动态规划的基本思想是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到目标问题的解。动态规划会保存已解决的子问题的答案，在求解目标问题的过程中，需要这些子问题答案时就可以直接利用，避免重复计算。 基于动态规划的强化学习算法主要有两种：一是策略迭代（policy iteration），二是价值迭代（value iteration）。其中，策略迭代由两部分组成：策略评估（policy evaluation）和策略提升（policy improvement）。具体来说，策略迭代中的策略评估使用贝尔曼期望方程来得到一个策略的状态价值函数，这是一个动态规划的过程；而价值迭代直接使用贝尔曼最优方程来进行动态规划，得到最终的最优状态价值。基于动态规划的这两种强化学习算法要求事先知道环境的状态转移函数和奖励函数，也就是需要知道整个马尔可夫决策过程。

策略迭代算法

策略评估

贝尔曼期望方程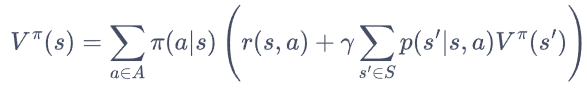： 当知道奖励函数和状态转移函数时，我们可以根据下一个状态的价值来计算当前状态的价值。因此，根据动态规划的思想，可以把计算下一个可能状态的价值当成一个子问题，把计算当前状态的价值看作当前问题。在得知子问题的解后，就可以求解当前问题。更一般的，考虑所有的状态，就变成了用上一轮的状态价值函数来计算当前这一轮的状态价值函数。

策略提升

总体来说，策略迭代算法的过程如下：对当前的策略进行策略评估，得到其状态价值函数，然后根据该状态价值函数进行策略提升以得到一个更好的新策略，接着继续评估新策略、提升策略……直至最后收敛到最优策略（收敛性有证明）

价值迭代算法

策略迭代中的策略评估需要进行很多轮才能收敛得到某一策略的状态函数，这需要很大的计算量，尤其是在状态和动作空间比较大的情况下。我们是否必须要完全等到策略评估完成后再进行策略提升呢？试想一下，可能出现这样的情况：虽然状态价值函数还没有收敛，但是不论接下来怎么更新状态价值，策略提升得到的都是同一个策略。 价值迭代算法，它可以被认为是一种策略评估只进行了一轮更新的策略迭代算法。需要注意的是，价值迭代中不存在显式的策略，我们只维护一个状态价值函数。

动态规划的主要思想是利用贝尔曼方程对所有状态进行更新。需要注意的是，在利用贝尔曼方程进行状态更新时，我们会用到马尔可夫决策过程中的奖励函数和状态转移函数。如果智能体无法事先得知奖励函数和状态转移函数，就只能通过和环境进行交互来采样（状态-动作-奖励-下一状态）这样的数据。