马尔可夫奖励过程
当且仅当某时刻的状态只取决于上一时刻的状态时,一个随机过程被称为具有马尔可夫性质。 也就是说,当前状态是未来的充分统计量,即下一个状态只取决于当前状态,而不会受到过去状态的影响。通过这种链式的关系,历史的信息被传递到了现在。马尔可夫性可以大大简化运算,因为只要当前状态可知,所有的历史信息都不再需要了,利用当前状态信息就可以决定未来。 状态转移矩阵:
\[\boldsymbol{P}=\left(\begin{array}{cccc} p\left(s_{1} \mid s_{1}\right) & p\left(s_{2} \mid s_{1}\right) & \ldots & p\left(s_{N} \mid s_{1}\right) \\ p\left(s_{1} \mid s_{2}\right) & p\left(s_{2} \mid s_{2}\right) & \ldots & p\left(s_{N} \mid s_{2}\right) \\ \vdots & \vdots & \ddots & \vdots \\ p\left(s_{1} \mid s_{N}\right) & p\left(s_{2} \mid s_{N}\right) & \ldots & p\left(s_{N} \mid s_{N}\right) \end{array}\right)\]给定一个马尔可夫过程,我们就可以从某个状态出发,根据它的状态转移矩阵生成一个状态序列(episode),这个步骤也被叫做采样(sampling)。
在马尔可夫过程的基础上加入奖励函数$r$ 和折扣因子$\gamma$,就可以得到马尔可夫奖励过程(Markov reward process)。
 在一个马尔可夫奖励过程中,从第$t$时刻状态$S_t$开始,直到终止状态时,所有奖励的衰减之和称为回报$G_t$
在马尔可夫奖励过程中,一个状态的期望回报(即从这个状态出发的未来累积奖励的期望)被称为这个状态的价值(value)。所有状态的价值就组成了价值函数(value function),价值函数的输入为某个状态,输出为这个状态的价值。我们将价值函数写成:
在一个马尔可夫奖励过程中,从第$t$时刻状态$S_t$开始,直到终止状态时,所有奖励的衰减之和称为回报$G_t$
在马尔可夫奖励过程中,一个状态的期望回报(即从这个状态出发的未来累积奖励的期望)被称为这个状态的价值(value)。所有状态的价值就组成了价值函数(value function),价值函数的输入为某个状态,输出为这个状态的价值。我们将价值函数写成:
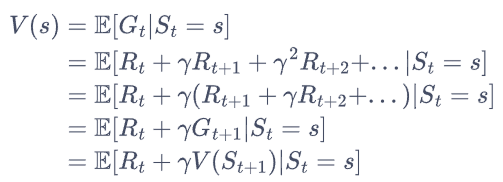
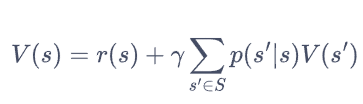 上式就是马尔可夫奖励过程中非常有名的贝尔曼方程(Bellman equation),对每一个状态都成立。
若一个马尔可夫奖励过程一共有个状态,我们将所有状态的价值表示成一个列向量,同理,将奖励函数写成一个列向量。于是我们可以将贝尔曼方程写成矩阵的形式:
上式就是马尔可夫奖励过程中非常有名的贝尔曼方程(Bellman equation),对每一个状态都成立。
若一个马尔可夫奖励过程一共有个状态,我们将所有状态的价值表示成一个列向量,同理,将奖励函数写成一个列向量。于是我们可以将贝尔曼方程写成矩阵的形式:
 以上解析解的计算复杂度是$O(n^3)$,因此这种方法只适用很小的马尔可夫奖励过程。求解较大规模的马尔可夫奖励过程中的价值函数时,可以使用动态规划(dynamic programming)算法、蒙特卡洛方法(Monte-Carlo method)和时序差分(temporal difference),这些方法将在之后的章节介绍。
以上解析解的计算复杂度是$O(n^3)$,因此这种方法只适用很小的马尔可夫奖励过程。求解较大规模的马尔可夫奖励过程中的价值函数时,可以使用动态规划(dynamic programming)算法、蒙特卡洛方法(Monte-Carlo method)和时序差分(temporal difference),这些方法将在之后的章节介绍。
马尔可夫决策过程
马尔可夫奖励过程(MRP)的基础上加入动作,就得到了马尔可夫决策过程(MDP) 。
我们不再使用类似 MRP 定义中的状态转移矩阵,而是直接使用状态转移函数。这样做一是因为此时的状态转移与动作也有关,变成了一个三维数组,而不再是一个矩阵(二维数组);二是因为状态转移函数更具有一般意义,例如,如果状态集合不是有限的,就无法用数组表示,但仍然可以用状态转移函数表示。
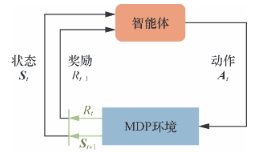 智能体的策略(policy)通常用字母$\pi$表示。表示在输入状态为 s 的情况下采取动作 a 的概率。当一个策略是确定性策略(deterministic policy)时,它在每个状态下只输出一个确定性的动作,即只有该动作的概率为 1,其他动作的概率为 0;当一个策略是随机性策略(stochastic policy)时,它在每个状态下输出的是关于动作的概率分布,然后根据该分布进行采样就可以得到一个动作。由于马尔可夫性质的存在,策略只需要与当前状态有关,不需要考虑历史状态。
智能体的策略(policy)通常用字母$\pi$表示。表示在输入状态为 s 的情况下采取动作 a 的概率。当一个策略是确定性策略(deterministic policy)时,它在每个状态下只输出一个确定性的动作,即只有该动作的概率为 1,其他动作的概率为 0;当一个策略是随机性策略(stochastic policy)时,它在每个状态下输出的是关于动作的概率分布,然后根据该分布进行采样就可以得到一个动作。由于马尔可夫性质的存在,策略只需要与当前状态有关,不需要考虑历史状态。
基于策略 $\pi$ 的状态价值函数, 表示从状态 s 出发遵循策略$\pi$能获得的期望回报:
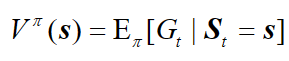 由于动作的存在,我们额外定义一个动作价值函数, 表示在 MDP 遵循策略$\pi$时,对当前状态 s 执行动作 a 得到的期望回报:
由于动作的存在,我们额外定义一个动作价值函数, 表示在 MDP 遵循策略$\pi$时,对当前状态 s 执行动作 a 得到的期望回报:
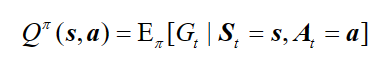 状态价值函数和动作价值函数之间的关系为:
状态价值函数和动作价值函数之间的关系为:
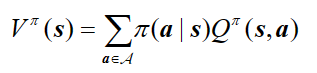 使用策略$\pi$时,在状态 s 下采取动作 a 的价值等于即时奖励加上经过衰减的所有可能的下一个状态的状态转移概率与相应的价值的乘积:
使用策略$\pi$时,在状态 s 下采取动作 a 的价值等于即时奖励加上经过衰减的所有可能的下一个状态的状态转移概率与相应的价值的乘积:
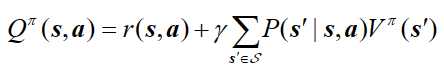 两个价值函数的贝尔曼期望方程:
两个价值函数的贝尔曼期望方程:
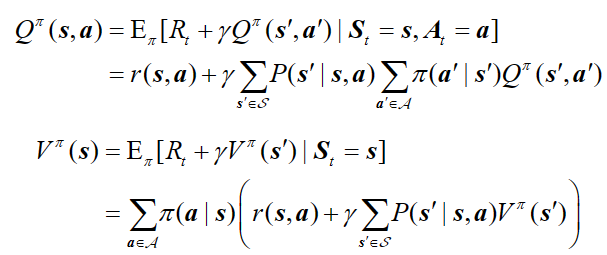 我们将策略的动作选择进行边缘化(marginalization),就可以得到没有动作的 MRP 了。具体来说,对于某一个状态,我们根据策略将所有动作的概率进行加权,得到的奖励和就可以被认为是一个 MRP 在该状态下的奖励,即
我们将策略的动作选择进行边缘化(marginalization),就可以得到没有动作的 MRP 了。具体来说,对于某一个状态,我们根据策略将所有动作的概率进行加权,得到的奖励和就可以被认为是一个 MRP 在该状态下的奖励,即
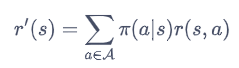
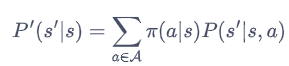
蒙特卡洛方法
一个状态的价值是它的期望回报,那么一个很直观的想法就是用策略在 MDP 上采样很多条序列,计算从这个状态出发的回报再求其期望就可以了:
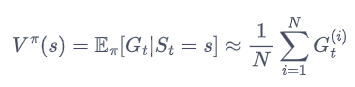
占用度量
我们需要理解不同策略会使智能体访问到不同概率分布的状态这个事实,这会影响到策略的价值函数。


最优策略


