光子带隙(Photonic Band Gap,简称PBG)是指在光子晶体中,特定频率范围内的电磁波(通常是可见光或近红外光)不能传播的现象。这一概念与电子在固体中的电子带隙相似,电子带隙是电子不能存在的能量区间。光子带隙是由光子晶体的周期性结构引起的,这种结构可以是一维、二维或三维的。
光子带隙的形成原理
光子带隙的形成基于布拉格散射原理,这是一种波在周期性结构中传播时遇到的散射现象。在光子晶体中,不同材料的周期性排列导致折射率的周期性变化。当入射光的波长与光子晶体的结构特征(如周期、层间距)相匹配时,光波会在晶体中多次反射和干涉,形成强烈的相干消减,从而禁止特定波长范围内的光波在晶体中传播。
数学表述
在数学上,光子带隙可以通过解析麦克斯韦方程组在周期性介质中的解来预测和分析。光子晶体的色散关系(即波矢与频率的关系)可以显示出禁带(带隙)。如果色散曲线在某个频率区间内没有交叉能带,那么该区间就是光子带隙。
应用
光子带隙的存在为许多光学应用提供了可能,包括但不限于:
- 光学滤波器:通过选择性允许特定频率的光通过,阻止其他频率的光。
- 波导:在光子晶体中创建缺陷(如移除一部分结构),可以在带隙中引导光波,因为光波倾向于留在允许其传播的区域。
- 激光器:在带隙中引入增益介质可以产生高效率的激光输出。
- 传感器:光子带隙结构对环境变化(如温度、压力、化学成分)非常敏感,可以用于高灵敏度的传感器。
布拉格散射的基本原理
布拉格散射的基本原理基于波的干涉效应。当波(如光波、声波或X射线)遇到具有周期性排列的层(例如晶体中的原子层)时,每一层都会散射波。如果散射波之间保持相干性,即相位差固定,这些波就会发生干涉。特定条件下,散射波会发生构造性干涉(相长干涉),导致强烈的反射波,这种情况称为布拉格反射。
布拉格定律
布拉格定律给出了发生布拉格反射的条件,可以用以下公式表示:
\[n\lambda = 2d\sin\theta\]其中:
- n 是一个整数,表示反射的级数(通常是1,称为第一级布拉格反射)。
- $\lambda$ 是入射波的波长。
- ( d ) 是晶体中相邻散射面之间的距离(即晶格常数)。
- $\theta$ 是入射波与晶体层的法线之间的角度。
当这一条件满足时,入射波的每次散射都在特定的角度上产生相长干涉,从而导致反射波的强度极大。
物理解释
布拉格散射可以这样形象理解:当入射波到达周期性结构(如晶格)时,每一层结构都像一个镜子一样反射波。当这些反射波的路径差是波长的整数倍时,即满足布拉格条件$n\lambda = 2d\sin\theta$时,各层反射的波完全相干地重叠,造成了反射波的强增强。反之,如果路径差不满足这个条件,不同层的反射波将因相位不匹配而发生相消干涉,导致反射波弱或不显著。
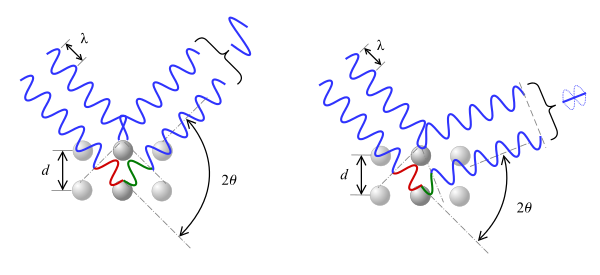
根据2𝜃推导,相位差会导致相长(图左)或相消(图右)干涉。
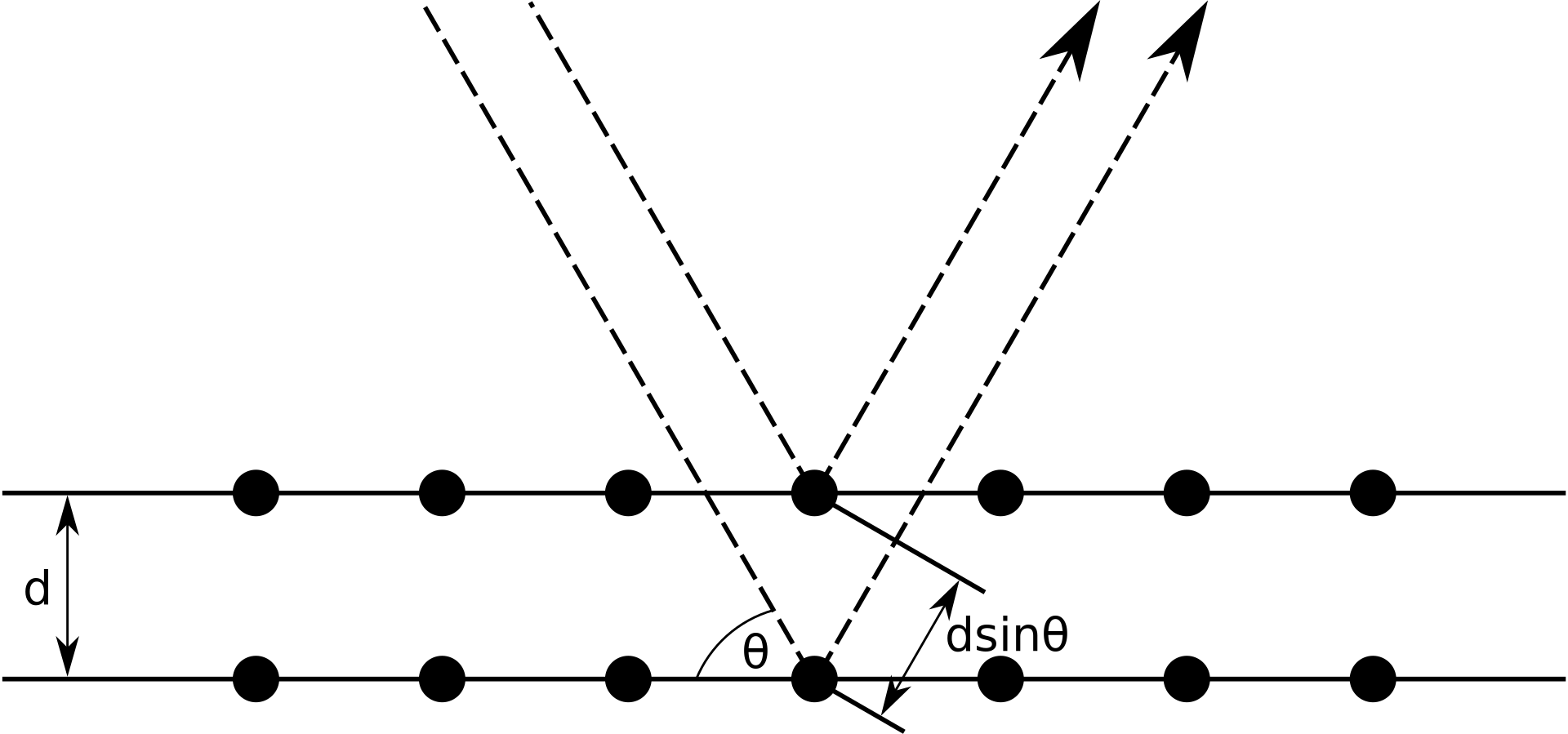
图为布拉格衍射。两束相同波长及相的辐射,向着固态晶体前进,最后被里面的两个原子所散射出去。下面的束被散射后,比上面的束多行了 2𝑑sin𝜃的距离。当这个距离等于辐射波长的倍数时,散射后的两束辐射就会产生相长干涉。
光子带隙的数学表述涉及到求解光子晶体的麦克斯韦方程组,并使用特定的边界条件和材料参数。这一过程中,主要的目标是找出光波在光子晶体中的色散关系,即频率与波矢(动量)之间的关系。这种关系可以揭示出光子带隙,也就是电磁波在某些频率范围内不能在晶体中传播的区域。
麦克斯韦方程在光子晶体中的表述
对于一个无源(无自由电荷和电流)的光子晶体,麦克斯韦方程简化为以下形式:
- 法拉第电磁感应定律:
- 安培定律(麦克斯韦修正):
- 高斯定律的电场和磁场表述:
其中,$\vec{E}$ 和 $\vec{H}$ 分别是电场和磁场,$\vec{D}$ 和$\vec{B}$ 分别是电位移场和磁感应强度。在光子晶体中,介电常数 $\epsilon$ 和磁导率 $\mu$ 可以是空间的周期函数,即 $\epsilon(\vec{r})$ 和 $\mu(\vec{r})$,表示材料属性的空间变化。
周期性边界条件与 Bloch-Floquet 定理
由于光子晶体具有周期性结构,可以应用Bloch-Floquet定理来简化问题。根据这个定理,电场和磁场可以表示为Bloch波形式:
\[\vec{E}(\vec{r}, t) = \vec{E}_k(\vec{r}) e^{i(\vec{k} \cdot \vec{r} - \omega t)}, \quad \vec{H}(\vec{r}, t) = \vec{H}_k(\vec{r}) e^{i(\vec{k} \cdot \vec{r} - \omega t)}\]其中,$\vec{E}_k(\vec{r})$ 和 $\vec{H}_k(\vec{r})$ 是周期性的函数,与光子晶体的晶格常数相同,$\vec{k}$ 是Bloch波矢,$\omega$ 是角频率。
寻找色散关系和带隙
通过将Bloch波形式代入麦克斯韦方程,并使用适当的数学技术(如平面波展开法或有限元法),可以得到一个本征值问题。求解这个本征值问题将给出色散关系$\omega(\vec{k})$,即频率与波矢的关系。色散关系的图形通常表现为频率与波矢的函数,其特定区域(无解区)显示为带隙,这些就是光子带隙。
Bloch-Floquet 定理
是固体物理学中一个核心原理,广泛应用于描述波在具有周期性结构的介质中的传播,如电子在晶格中的行为和光波在光子晶体中的传播。这个定理说明,在周期性的势场中,波函数可以表示为一个周期函数与一个平面波的乘积。这一理论对理解电子带结构、光子带隙和声子带隙等现象至关重要。
定理的数学表述
Bloch-Floquet 定理表明,如果一个系统具有空间周期性,那么系统的波函数(可以是电子的波函数、光波或声波)可以写为一个周期性因子和一个复指数因子的乘积。这个形式通常表示为:
\[\psi_{\vec{k}}(\vec{r}) = e^{i \vec{k} \cdot \vec{r}} u_{\vec{k}}(\vec{r})\]其中:
- $\psi_{\vec{k}}(\vec{r})$ 是波函数,
- $\vec{k}$ 是Bloch波矢,一个与晶体的周期性结构相关的参数,
- $u_{\vec{k}}(\vec{r})$ 是一个与晶体的周期相同的周期性函数,
- $e^{i \vec{k} \cdot \vec{r}}$ 是一个平面波。
在光子晶体中,波矢(wave vector)是一个描述电磁波相位随空间变化的矢量,通常表示为$\vec{k}$。波矢的大小和方向描述了电磁波在空间中的传播特性,包括传播方向和波长(或空间频率)。
波矢的定义
波矢 $\vec{k}$ 定义为电磁波的相位梯度,即
\[\vec{k} = \nabla \phi\]其中 $\phi$是波的相位。在周期性介质中,例如光子晶体,波的相位和振幅通常具有周期性变化的特性。 波矢反应传播方向和角频率。
Bloch-Floquet 定理与波矢
根据Bloch-Floquet 定理,光子晶体中的电磁波可以表示为一个平面波和一个周期函数的乘积,形式为:
\[\psi(\vec{r}) = e^{i \vec{k} \cdot \vec{r}} u_{\vec{k}}(\vec{r})\]这里,$e^{i \vec{k} \cdot \vec{r}}$ 是表示波的传播部分,而 $u_{\vec{k}}(\vec{r})$ 是与晶体结构具有相同周期性的函数。在这种表述中,$\vec{k}$ 就是Bloch波矢,它决定了波的传播方向和相位变化速度。 波矢在狭义相对论背景下可定义为四维矢量。
波矢在光子晶体中的角色
光子晶体中的波矢 $\vec{k}$ 对于理解和设计光子带隙结构至关重要。波矢的大小和方向不仅决定了波在光子晶体中的传播路径,还影响到光波与晶体结构的相互作用,从而影响到带隙的形成和位置。通过精确调控光子晶体的结构参数,如周期和折射率的分布,可以对特定方向和波长的光波进行选择性的反射或传输,实现高效的光控制和操纵。
